在我国古代数学名著

在我国古代数学名著

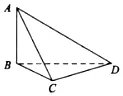
在我国古代数学名著九章算术中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,平面BCD,且,则异面直线AC与BD所成角的余弦值为( )

在我国古代数学名著九章算术中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,平面BCD,且,则异面直线AC与BD所成角的余弦值为( )

在我国古代数学名著九章算术中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,平面BCD,且,则异面直线AC与BD所成角的余弦值为( )

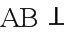
在我国古代数学名著九章算术中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,平面BCD,且,则异面直线AC与BD所成角的余弦值为( )

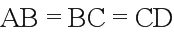
在我国古代数学名著九章算术中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,平面BCD,且,则异面直线AC与BD所成角的余弦值为( )

A. B. C. D.

A. B. C. D.

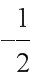
A. B. C. D.

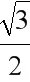
A. B. C. D.

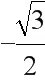
[答案]A

[解析]如图,分别取的中点,连,

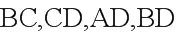
[解析]如图,分别取的中点,连,

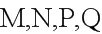
[解析]如图,分别取的中点,连,

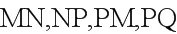
[解析]如图,分别取的中点,连,

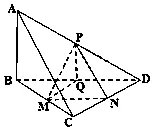
则,

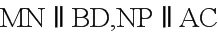
则,

∴即为异面直线和所成的角(或其补角).

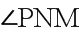
∴即为异面直线和所成的角(或其补角).

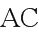
∴即为异面直线和所成的角(或其补角).

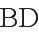
∴即为异面直线和所成的角(或其补角).

又由题意得,.

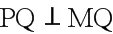
又由题意得,.

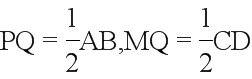
又由题意得,.

设,则.

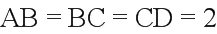
设,则.

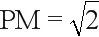
设,则.

又,

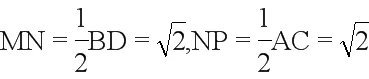
又,

∴为等边三角形,

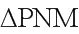
∴为等边三角形,

∴,

∴,

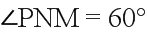
∴异面直线AC与BD所成角为,其余弦值为.选A.

∴异面直线AC与BD所成角为,其余弦值为.选A.

∴异面直线AC与BD所成角为,其余弦值为.选A.

点睛:

用几何法求空间角时遵循“一找、二证、三计算”的步骤,即首先根据题意作出所求的角,并给出证明,然后将所求的角转化为三角形的内角.解题时要注意空间角的范围,并结合解三角形的知识得到所求角的大小或其三角函数值.